Bending the Truth.

Eratosthenes of Cyene.

Eratosthenes of Cyrene c. 276 BC – c. 195/194 BC) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to what is now known as the study of geography, and he (allegedly) introduced some of the terminology still used today.

He is best known for being the first person known to calculate the circumference of the Earth, which he did by using the extensive survey results he could access in his role at the Library; his calculation was remarkably accurate. He was also the first to calculate Earth's axial tilt, which also proved to have remarkable accuracy. He created the first global projection of the world, incorporating parallels and meridians based on the available geographic knowledge of his era.

Eratosthenes was the founder of scientific chronology; he endeavoured to revise the dates of the main events of the semi-mythological Trojan War, dating the Sack of Troy to 1183 BC. In number theory, he introduced the sieve of Eratosthenes, an efficient method of identifying prime numbers.

The measurement of Earth's circumference is the most famous among the results obtained by Eratosthenes, who estimated that the meridian has a length of 252,000 stadia (39,060-40,320 km), with an error on the real value between −2.4% and +0.8% (assuming a value for the stadion between 155 and 160 metres). Eratosthenes described his arc measurement technique, in a book entitled On the measure of the Earth, which has not been preserved. However, a simplified version of the method has been preserved, as described by Cleomedes.

The simplified method works by considering two cities along the same meridian and measuring both the distance between them and the difference in angles of the shadows cast by the sun on a vertical rod (a gnomon) in each city at noon on the summer solstice. The two cities used were Alexandria and Syene (modern Aswan), and the distance between the cities was measured by professional bematists. A geometric calculation reveals that the circumference of the Earth is the distance between the two cities divided by the difference in shadow angles expressed as a fraction of one turn.

Key points:

1. His book 'On the measure of the Earth', has not survived. All that is allegedly available, is a simplified version which is attributed to Cleomedes.

2. A 'bematist' is a person who physically walks across the ground and keeps a record of how many paces it has taken to traverse a set distance.

3. There is no evidence of a mechanical device like a surveyors wheel being used.

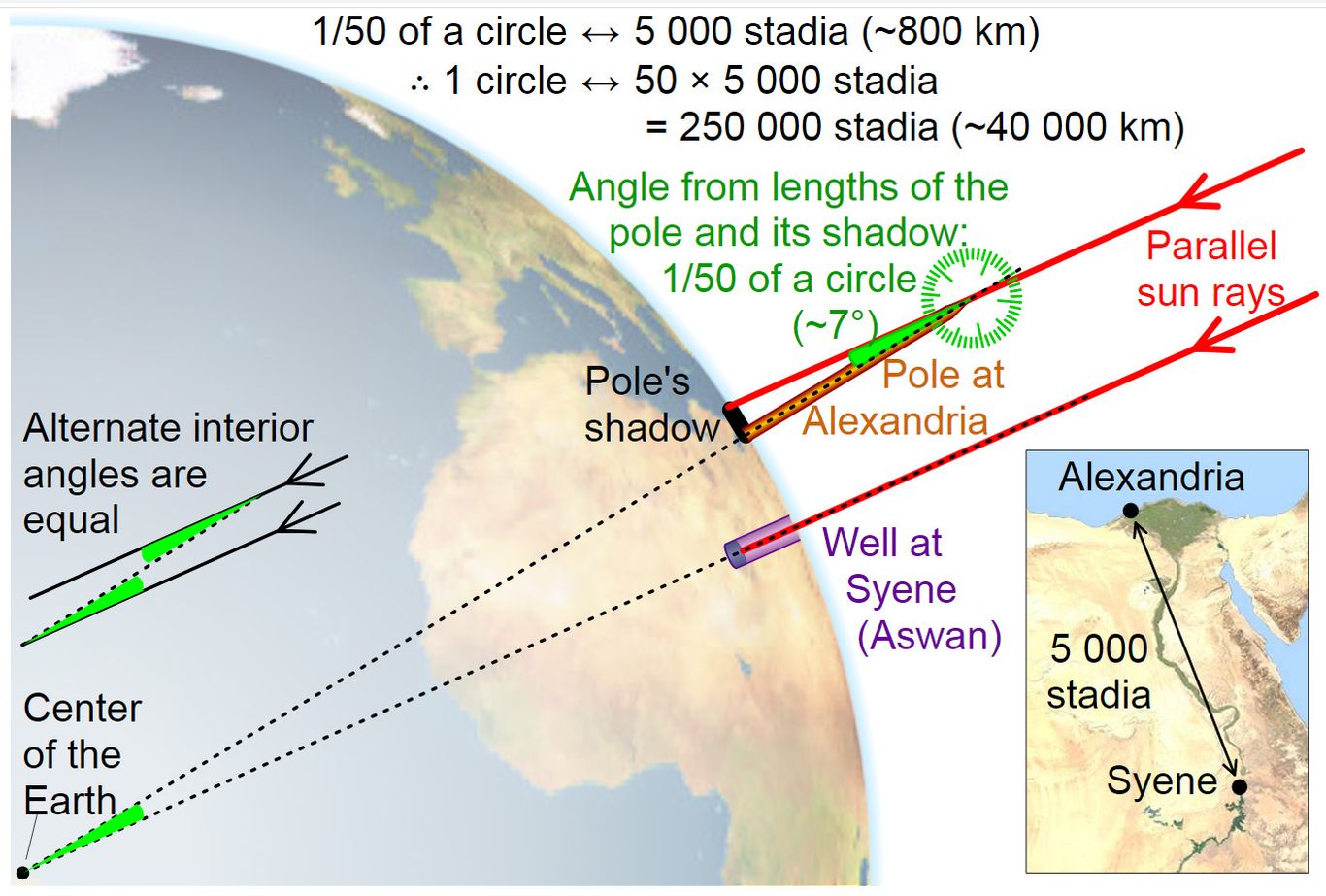
4. The distance between Alexandria and Syene is stated to be 5,000 stadia, which is equivalent to 497 miles or 800 kilometers.

5. One Greek 'stadion' was said to be equivalent to 600 'Ancient Greek feet'.

6. In order to calculate the distance between Alexandria and Syene, a person had to walk on foot between the two locations.

7. This distance should have already been known as maps would have been available for merchants and the like, so why was it necessary to check again?

8. The experiment requires that the observer in Alexandria and the observer in Syene perform the experiment at precisely the same time.

How was that achieved without accurate clocks or modern mobile communication devices like phones?

https://www.bing.com/search?q=Eratosthenes&FORM=AWRE

Measuring Shadows.

The experiment relies on the proposition that the sun's rays are parallel when they strike the earth; but the sun emits rays radially in all directions, so the way round this is to claim that because the sun is so far away, the rays are 'almost' parallel when they strike the earth.

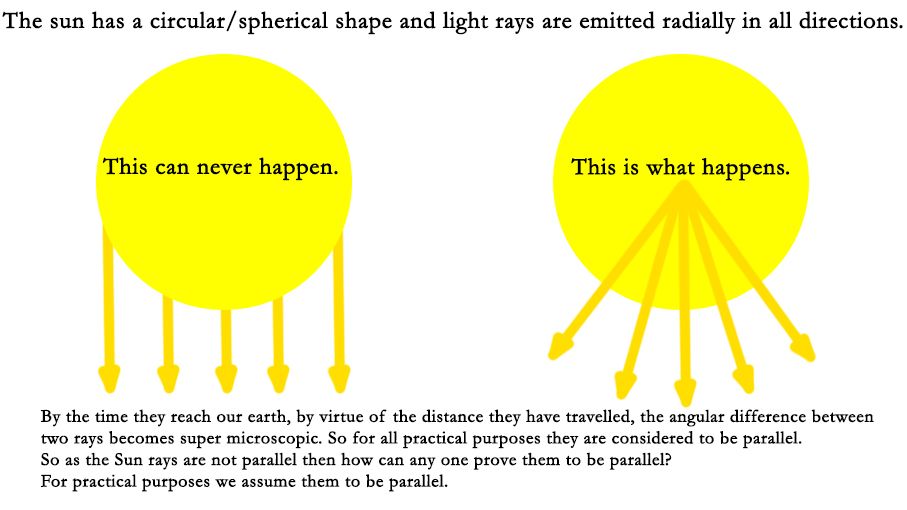
THE KEY POINT IS THAT THE LIGHT RAYS ARE ASSUMED TO BE PARALLEL, BUT THIS IS NOT THE TRUTH.

In the NASA sponsored documentary called 'Cosmos', Carl Sagan discussed the experiment as allegedly performed by Eratosthenes.

He held a large map of the area made of thick card that had two small, wooden obelisks glued to the location at Alexandria and Syene. He explained:

"If at a certain moment, each stick casts no shadow, that's perfectly easy to understand provided the earth is flat".

He continued:

"If the shadow at Syene is a certain length and the shadow at Alexandria is the same length; that also makes sense on a flat earth. "But how could it be", Eratosthenes asked "That there was no shadow at Syene and a very substantial shadow at Alexandria?". The only answer is that the surface of the earth is curved. Not only that, but the greater the curvature, the bigger the difference in the lengths of the shadows.

The sun is so far away its rays are parallel when they reach the earth. Sticks at different angles to the sun's rays will cast shadows at different lengths. But the observed difference in these shadow lengths - the distance between Alexandria and Syene, had to be about seven degrees along the surface of the earth.

By that I mean, if you imagine these sticks (obelisks stuck on the map) extending all the way to the centre of the earth, they would intersect at an angle of about seven degrees. This is about one fiftieth of the circumference of the earth - 360 degrees.

Eratosthenes knew the distance between Alexandria and Syene; he knew it was 800 kilometres because he hired a man to pace out the distance in order to perform the calculation. 800 times 50 is 40,000, so that must be the circumference of the earth. Eratosthenes' only tools were sticks, size, feet and brains"

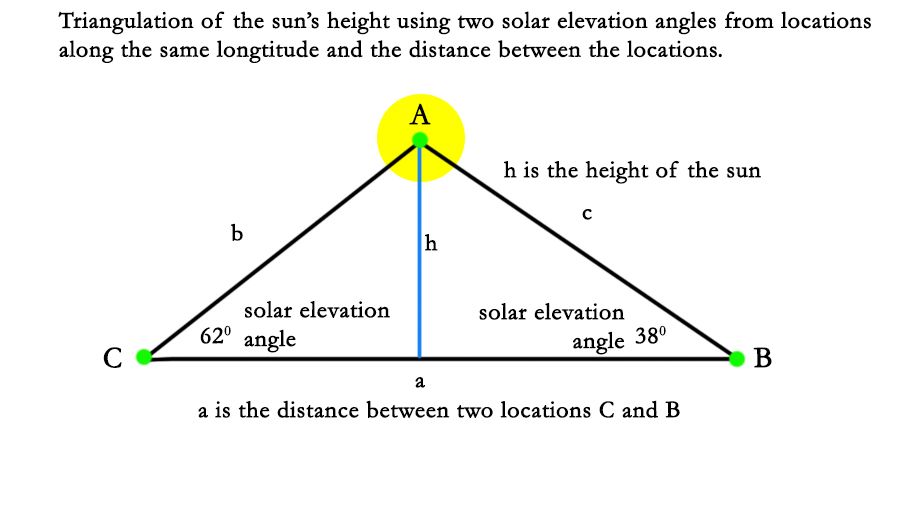
How far away is the sun?

In order to work out how far away the sun is, you can use a method called triangulation.

For example, if both angles were 75 degrees and the distance between the two locations was 2,074 miles, the distance to the sun will be 3,870 miles.